La conductivité électrique1
1) Définition
La conductivité électrique caractérise l’aptitude d’un matériau ou d’une solution à laisser les charges électriques se déplacer librement et donc permettre le passage d’un courant électrique. Ce paramètre se mesure avec un conductimètre. Dans le SI (Système International d’Unités), la conductivité est mesurée en S.m-1 (siemens par mètre), mais le plus souvent la mesure avec un conductimètre donne le résultat en mS.cm-1 (millisiemens par centimètre) ou en μS. cm-1 (microsiemens par centimètre)2.
2) Les électrolytes
Un électrolyte est une substance qui produit une solution conductrice de l’électricité quand elle est dissoute dans un solvant polaire, comme l’eau. Les solutions ioniques conduisent le courant électrique. Le passage du courant dans la solution est dû à la circulation des ions :
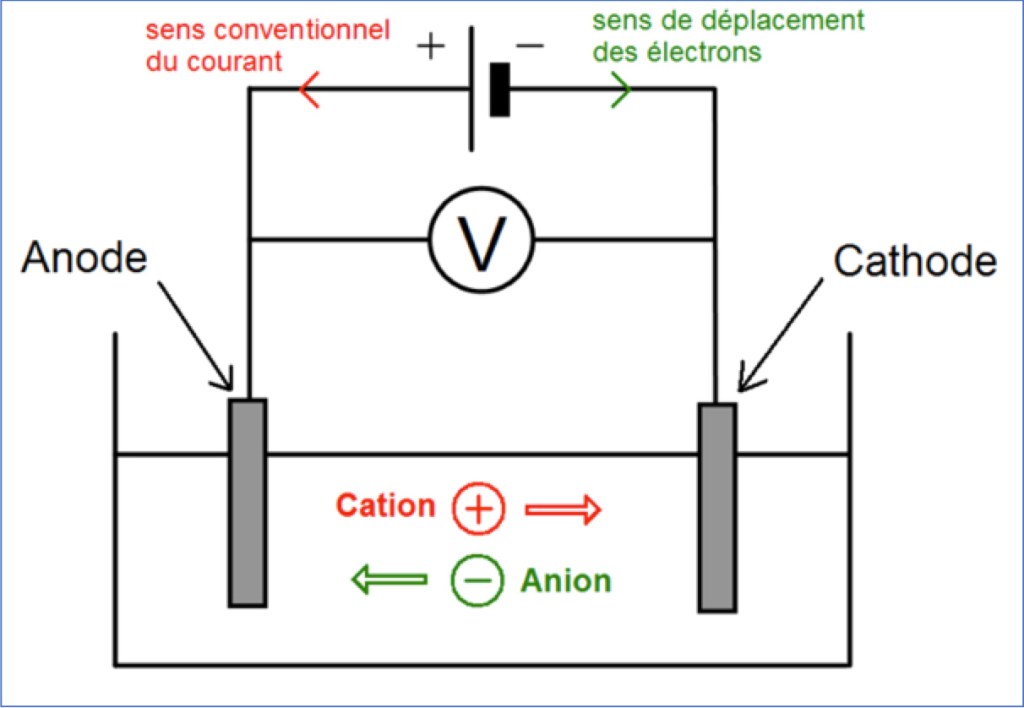
- les cations, chargés positivement, circulent de la borne + du générateur vers la borne – (dans le sens conventionnel du courant)
- les anions, chargés négativement, circulent de la borne – du générateur vers la borne + (dans le sens inverse du sens conventionnel du courant).
L’électrode vers laquelle se dirigent les cations est appelée « cathode », et celle vers laquelle se dirigent les anions est appelée « anode ».
Remarque
Les concentrations de substances qui ne s’ionisent pas en solution aqueuse (non-électrolytiques), comme le saccharose (sucre alimentaire) par exemple, ne sont pas mesurables par conductimétrie.
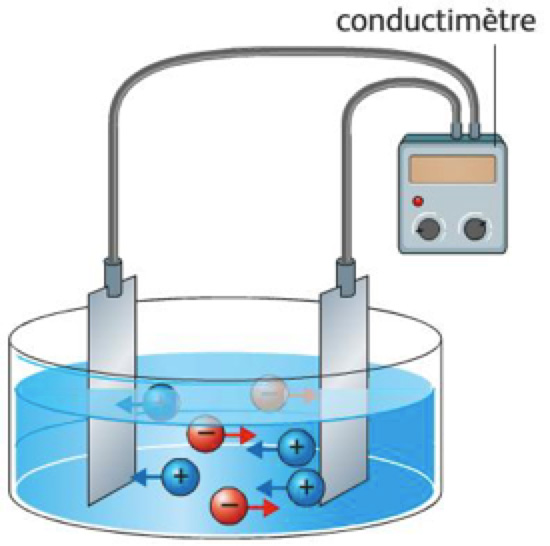
3) Le conductimètre
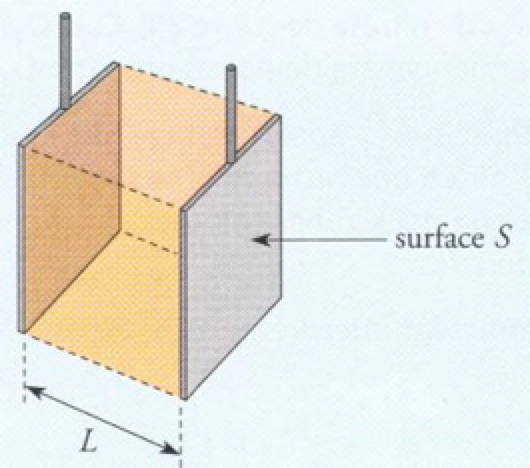
Une cellule de conductimétrie (ci-contre) est constituée de deux plaques (les électrodes) identiques et parallèles, de surface S (m2) et d’écartement L (m), reliées à un générateur de tension alternative (∼ 500 Hz, pour éviter l’altération des électrodes et leur polarisation). On appelle conductance de la portion de solution comprise entre les électrodes, l’inverse de la résistance R (ohm). Elle se note G et s’exprime en Siemens (symbole : S)
avec
, ρ étant la résistivité de la solution
est la conductivité de la solution
⇒ et
avec
= constante de cellule
k s’exprime en m-1 et σ en S.m-1
La cellule de mesure est connectée au conductimètre proprement dit qui mesure la conductance de la solution3. Cet appareil est composé d’un générateur basse fréquence (courant alternatif), d’un ampèremètre et d’un voltmètre. Cette technique a été développée par Friedrich Kohlrausch en 1874.

Pour des solutions peu concentrées, la conductance est proportionnelle à la concentration molaire c en soluté, exprimée en mol.m-3 (et non en mol.L-1 !). On obtient :
G = K x c et σ = k x G
On en déduit donc que la conductivité σ est proportionnelle à la concentration c en soluté (k dépendant des caractéristiques géométriques de la cellule).
Le facteur de proportionnalité dépend de la constante de cellule, de la nature du soluté et de la température.
Dans une cellule de conductimétrie, la constante de cellule est en général fournie par le constructeur et le conductimètre possède un système de compensation pour la température. La seule inconnue restante est la nature du soluté.
4) Conductivité molaire ionique
Pour une solution ionique peu concentrée, la conductivité σ de la solution est proportionnelle à la concentration. Le rapport de proportionnalité s’appelle la conductivité molaire du soluté, elle se note Λ et s’exprime en siemens.mètre carré par mole (symbole : S.m².mol–1) :
σ = Λ x C
avec:
Λ : conductivité molaire du soluté (en S.m².mol-1)
c : concentration molaire du soluté (en mol.m-3)
σ : conductivité de la solution (en S.m-1)
On montre que la conductivité molaire d’un électrolyte en solution diluée résulte de la somme de plusieurs termes (indépendants l’un de l’autre), chacun d’eux correspond à la contribution de l’un des ions à la conductivité de la solution. Ainsi, on peut mettre la conductivité molaire d’un soluté AaBb sous la forme :
AaBb (s) → aAx+(aq) + bBy-(aq)

5) Loi de Kohlrausch
La valeur de la conductivité σ d’une solution peut être calculée à partir des conductivités molaires ioniques λi des ions qui contribuent à la conductivité de la solution, ainsi que de leur concentration [Xi] :
σ = Σ ⎢zi ⎢ λi [Xi]
[Xi] : concentration molaire de l’ion i (en mol.m-3 !)
λi : conductivité molaire ionique de l’ion i (en S.m2.mol-1; ces valeurs sont données dans des tables)
zi : le nombre de charges portées par l’ion i, indépendamment de son signe. Cette formule n’est valable que pour des solutions diluées de concentration < 10-2 mol.L-1.
Remarque
Les ions H3O+ et HO– contribuent aussi à la conductivité de la solution et leurs conductivités molaires ioniques sont particulièrement élevées, mais, si le pH de la solution avoisine la neutralité, leurs concentrations sont faibles (≈10-4 mol.m-3) et on peut les négliger lors des calculs.
Exemple
Quelle est la conductivité d’une solution aqueuse où l’on a dissous du chlorure de sodium et du chlorure de potassium ?
Ions présents en solution : Na+(aq), K+(aq), Cl–(aq), H3O+(aq) et HO–(aq)
Conductivité de la solution : σ = (λNa+ x [Na+]) + (λK+ x [K+]) + (λCℓ– x [Cℓ–]) + (λH3O+ x [H3O+]) + (λHO– x [HO–])
| Ions | H3O+ | OH– | Cl– | K+ | Na+ |
|---|---|---|---|---|---|
| λ (S.m2.mol-1) à 25 ° C | 35,0.10–3 | 20,0.10–3 | 7,63.10–3 | 7,35.10–3 | 5,00.10–3 |
À pH 7, la conductivité théorique de l’eau « pure » est de :
(10-4 x 35.10-3) + (10-4 x 20.10-3) = 55.10-7 S.m-1 = 0,055 μS.cm-1
Dans l’industrie pharmaceutique, par des techniques de purification très poussées, on parvient à atteindre des valeurs proches de 1 μS.cm-1.
Notes & Références
- Inspiré de : http://spc.emde.free.fr/fichiers/terminale_spe/Chapitre_2.pdf
- 1 S.m-1 = 0,01 S.cm-1 = 10 mS.cm-1 = 10000 μS.cm-1
- En fait, du volume de solution situé entre les électrodes de la cellule de conductimétrie.
